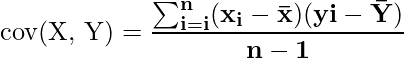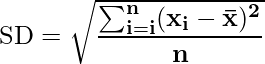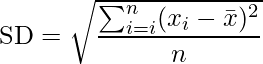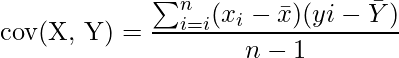It’s essential to evaluate the sensible significance or real-world influence of the findings along with the statistical significance of the findings when doing analysis or analyzing experimental knowledge. The thought of impact magnitude is then related on this scenario. Researchers can quantify and talk about the applying of their findings through the use of the standardized measure of impact measurement to explain the dimensions of the noticed impact.
Estimating and understanding impact sizes rely closely on impact measurement formulae. These equations are meant to condense the magnitude of variations between teams or the power and course of the hyperlink between variables. Researchers can enhance the reproducibility of their findings, higher perceive the importance of their discoveries, and make clever judgments by measuring the impact measurement.
What’s Impact Measurement?
The Idea of “impact Measurement ” in statistics measures the extent or power of a relationship between two variables or the excellence between two teams. It signifies how a lot a specific remedy, intervention, or issue influences a desired outcome. The impact measurement is useful as a result of it allows lecturers and practitioners to know the sensible significance or real-world value of their findings.
What’s Impact Measurement Formulation?
We use Cohen’s D methodology to compute how carefully two variables are associated:
Impact Measurement = (M1 – M2)/SD
the place,
- M1 is the imply of the primary inhabitants group,
- M2 is the imply of the second inhabitants group, and
- SD is the usual deviation.
Interpretation of Impact Measurement
Impact Sizes: Utilizing standardized standards, impact sizes could be divided into three classes: small, medium, and large. Quite a few definitions of minor, medium, and enormous results could also be relevant relying on the circumstance and the analysis subject.
Along with statistical significance, impact measurement additionally contributes to assessing the sensible significance or value of the outcomes. A outcome could not all the time have a huge impact measurement even whether it is statistically important, and the other can be true. Each statistical and sensible significance should be thought of whereas inspecting knowledge.
Forms of Impact Measurement
Impact Sizes are categorized into so many varieties, The intention of every of which is to measure the connection between two variables. Probably the most used sorts of impact sizes are:
- Cohen’s d
- Pearson’s r
- Odds Ratio
- Phi Coefficient
Let’s talk about these sorts intimately as follows:
Cohen’s d
The standardized distinction between two means is measured on this.
Cohen’s d = M1 – M2 / SD
The place,
- d is the efficient measurement,
- M1 is the imply of the primary inhabitants group,
- M2 is the imply of the second inhabitants group, and
- SD is the usual deviation.
- SD = √{(SD12 + SD22) ⁄ 2}
- The place SD1 and SD2 are the Normal deviation of first and second popilation group.
Pearson’s r
It Calculates how strongly two variables are correlated linearly.
Pearson’s r = cov(X,Y)/(SDx × SDy)
The place,
- cov(X,Y) is covarience between Xand Y,
- SDx is customary deviation of X, and
- SDy is customary deviation of Y.
Odds Ratio
This calculates the chance that an occasion will happen in a single group vs one other and is given as follows:
Odds Ratio = (a/b)/(c/d)
The place a,b,c, and d are frequencies of two × 2 desk.
Phi Coefficient
This gauges how strongly two binary variables are associated, and mathematically given by:
Phi Coefficient = (advert – bc) / √{(a+b)(c+d)(a+c)(b+d)}
The place a,b,c, and d are frequencies of two × 2 desk.
Solved Examples of Impact Measurement Formulation
Instance 1: Two teams of scholars’ take a look at outcomes had been in contrast in a examine. Group B obtained a median rating of 85 whereas Group A obtained a median rating of 80. The pooled customary deviation was calculated as 10. Decide the impact measurement utilizing Cohen’s d.
Reply:
Given: M1 = 80, M2 = 85, and SD = 10
Utilizing the formulation, d = (M1 – M2) / SD
⇒ d = (80 – 85) / 10
⇒ d = -5 / 10= -0.5
The impact measurement, on this case, is -0.5.
Instance 2: A standardized nervousness scale was utilized in a examine to check the nervousness ranges of two teams. Group X scored a median of 35, whereas Group Y scored a median of 40. The calculated pooled customary deviation was 6.5. Utilizing Cohen’s d, decide the impact magnitude.
Reply:
Given: M1 = 35, M2 = 40, and SD = 6
Utilizing the formulation, d = (M1 – M2) / SD
⇒ d = (35 – 40) / 6.5
⇒ d = -5 / 6.5≈ -0.769
The impact measurement for this examine is roughly -0.769.
Instance 3: Contemplate two teams of scholars, Group A and Group B, with the next marks in a GFG contest. Decide the impact measurement utilizing Cohen’s d.
Reply:
Step 1: Firstly we have now to find out Imply of Two Teams
By including up the marks for every group and dividing by the full variety of college students, we will first decide the imply for every group:
Group A’s imply (M1) is (78 + 82 + 85 + 90 + 73) / 5 = 81.6
Group B’s imply (M2) is (65 + 70 + 68 + 75 + 72) / 5 = 70
Step 2:Right here we’re suppose to calculate the usual deviation.
For Group A: Varience Of Group A: 33.840
Group A’s customary deviation (SDx) is 5.817.
For Group B: Varience Of Group B: 11.6
Group B’s customary deviation (SDy) is 3.406.
Step 3: calculating pooled customary deviation (SD)
Utilizing the formulation for the pooled customary deviation
SD = √{(SD12 + SD22) ⁄ 2}
⇒ SD ≈ 4.77
Step 4: Figuring out the impact measurement utilizing Cohen’s d.
For Cohen’s d: Distinction = M1 – M2 = 81.6 – 70 = 11.6
d = Distinction / SD = 11.6 /4.7665 = 2.434
The impact measurement, for this comparability of Group A and Group B arithmetic examination scores is roughly 2.434 .
Instance 4: Decide Pearson’s r utilizing the knowledge beneath:
- X: 1, 2, 3, 4, 5
- Y: 2, 4, 6, 8, 10
Reply:
As
Thus, SDx = 3, and SDy = 6
and
⇒ cov(X, Y) = 4
And, r = cov(X,Y)/(SDx × SDy)
⇒ r = 4/{3 × 6}
⇒ r = 4/18
⇒ r = 0.222 . . .
Instance 5: For the next info, decide the percentages ratio:
- Group 1: 20 victories, 30 failures
- Group 2: 20 failures, 30 triumphs
Reply:
Odd Ratios of data is; OR = (20/30) / (30/20) = 4/3
Instance 6: Decide the phi coefficient for the given info:
a = 10, b = 20, c = 30, d = 40
Reply:
phi = (1040 – 2030) / sqrt((10 + 20 )(30 + 40 )(10 + 30)*(20 +))phi = 0.22.
FAQs on Impact Measurement Formulation
Q1: Which Impact Measurement is Best?
Reply:
The examine’s setting will decide an appropriate impact measurement. Usually talking, an influence measurement of 0.2 is considered minor, 0.5 as medium, and 0.8 or above as massive.
Q2: How ought to Impact Measurement be Interpreted?
Reply:
The examine’s context impacts how impact measurement must be interpreted. A bigger impact measurement sometimes denotes a stronger correlation between two variables or a better hole between two teams.
Q3: What distinguishes Statistical Significance from Impact Measurement?
Reply:
Impact measurement calculates the dimensions of the distinction between two teams or the power of the correlation between two variables, versus statistical significance, which evaluates the chance that the noticed distinction or relationship just isn’t the results of probability.
This autumn: Can Impact Measurement Have a Dangerous Impact?
Reply:
Impact measurement can, actually, be dangerous. The 2 teams being in contrast are extra comparable than distinct when the impact magnitude is destructive.
Q5: What Profit Does Using Impact Measurement Present?
Reply:
The benefit of utilizing impact measurement is that it offers a dependable technique to gauge how a lot two teams differ or how strongly two variables are related. This makes it doable for researchers to judge the consequences of various interventions or therapies in a wide range of trials.
Q6: What downside Exists with regard to Impact Measurement?
Reply:
The downside of impact measurement is that it’s unable to inform us whether or not the noticed distinction or affiliation is statistically important.