About six months in the past, we confirmed how you can create a customized wrapper to acquire uncertainty estimates from a Keras community. Right this moment we current a much less laborious, as effectively faster-running method utilizing tfprobability, the R wrapper to TensorFlow Chance. Like most posts on this weblog, this one received’t be quick, so let’s rapidly state what you may anticipate in return of studying time.
What to anticipate from this submit
Ranging from what not to anticipate: There received’t be a recipe that tells you the way precisely to set all parameters concerned with a purpose to report the “proper” uncertainty measures. However then, what are the “proper” uncertainty measures? Except you occur to work with a way that has no (hyper-)parameters to tweak, there’ll all the time be questions on how you can report uncertainty.
What you can anticipate, although, is an introduction to acquiring uncertainty estimates for Keras networks, in addition to an empirical report of how tweaking (hyper-)parameters could have an effect on the outcomes. As within the aforementioned submit, we carry out our checks on each a simulated and an actual dataset, the Mixed Cycle Energy Plant Information Set. On the finish, instead of strict guidelines, it’s best to have acquired some instinct that can switch to different real-world datasets.
Did you discover our speaking about Keras networks above? Certainly this submit has an extra aim: To date, we haven’t actually mentioned but how tfprobability goes along with keras. Now we lastly do (briefly: they work collectively seemlessly).
Lastly, the notions of aleatoric and epistemic uncertainty, which can have stayed a bit summary within the prior submit, ought to get way more concrete right here.
Aleatoric vs. epistemic uncertainty
Reminiscent someway of the basic decomposition of generalization error into bias and variance, splitting uncertainty into its epistemic and aleatoric constituents separates an irreducible from a reducible half.
The reducible half pertains to imperfection within the mannequin: In concept, if our mannequin had been excellent, epistemic uncertainty would vanish. Put in another way, if the coaching knowledge had been limitless – or in the event that they comprised the entire inhabitants – we may simply add capability to the mannequin till we’ve obtained an ideal match.
In distinction, usually there’s variation in our measurements. There could also be one true course of that determines my resting coronary heart price; nonetheless, precise measurements will differ over time. There’s nothing to be completed about this: That is the aleatoric half that simply stays, to be factored into our expectations.
Now studying this, you may be pondering: “Wouldn’t a mannequin that truly had been excellent seize these pseudo-random fluctuations?”. We’ll go away that phisosophical query be; as a substitute, we’ll attempt to illustrate the usefulness of this distinction by instance, in a sensible method. In a nutshell, viewing a mannequin’s aleatoric uncertainty output ought to warning us to think about applicable deviations when making our predictions, whereas inspecting epistemic uncertainty ought to assist us re-think the appropriateness of the chosen mannequin.
Now let’s dive in and see how we could accomplish our aim with tfprobability. We begin with the simulated dataset.
Uncertainty estimates on simulated knowledge
Dataset
We re-use the dataset from the Google TensorFlow Chance workforce’s weblog submit on the identical topic , with one exception: We prolong the vary of the impartial variable a bit on the unfavourable aspect, to raised exhibit the totally different strategies’ behaviors.
Right here is the data-generating course of. We additionally get library loading out of the way in which. Just like the previous posts on tfprobability, this one too options lately added performance, so please use the event variations of tensorflow and tfprobability in addition to keras. Name install_tensorflow(model = "nightly") to acquire a present nightly construct of TensorFlow and TensorFlow Chance:
# be sure that we use the event variations of tensorflow, tfprobability and keras
devtools::install_github("rstudio/tensorflow")
devtools::install_github("rstudio/tfprobability")
devtools::install_github("rstudio/keras")
# and that we use a nightly construct of TensorFlow and TensorFlow Chance
tensorflow::install_tensorflow(model = "nightly")
library(tensorflow)
library(tfprobability)
library(keras)
library(dplyr)
library(tidyr)
library(ggplot2)
# be sure that this code is appropriate with TensorFlow 2.0
tf$compat$v1$enable_v2_behavior()
# generate the information
x_min <- -40
x_max <- 60
n <- 150
w0 <- 0.125
b0 <- 5
normalize <- perform(x) (x - x_min) / (x_max - x_min)
# coaching knowledge; predictor
x <- x_min + (x_max - x_min) * runif(n) %>% as.matrix()
# coaching knowledge; goal
eps <- rnorm(n) * (3 * (0.25 + (normalize(x)) ^ 2))
y <- (w0 * x * (1 + sin(x)) + b0) + eps
# take a look at knowledge (predictor)
x_test <- seq(x_min, x_max, size.out = n) %>% as.matrix()How does the information look?
ggplot(knowledge.body(x = x, y = y), aes(x, y)) + geom_point()
Determine 1: Simulated knowledge
The duty right here is single-predictor regression, which in precept we will obtain use Keras dense layers.
Let’s see how you can improve this by indicating uncertainty, ranging from the aleatoric sort.
Aleatoric uncertainty
Aleatoric uncertainty, by definition, shouldn’t be an announcement concerning the mannequin. So why not have the mannequin be taught the uncertainty inherent within the knowledge?
That is precisely how aleatoric uncertainty is operationalized on this method. As a substitute of a single output per enter – the anticipated imply of the regression – right here we’ve two outputs: one for the imply, and one for the usual deviation.
How will we use these? Till shortly, we’d have needed to roll our personal logic. Now with tfprobability, we make the community output not tensors, however distributions – put in another way, we make the final layer a distribution layer.
Distribution layers are Keras layers, however contributed by tfprobability. The superior factor is that we will prepare them with simply tensors as targets, as typical: No must compute chances ourselves.
A number of specialised distribution layers exist, equivalent to layer_kl_divergence_add_loss, layer_independent_bernoulli, or layer_mixture_same_family, however essentially the most normal is layer_distribution_lambda. layer_distribution_lambda takes as inputs the previous layer and outputs a distribution. So as to have the ability to do that, we have to inform it how you can make use of the previous layer’s activations.
In our case, in some unspecified time in the future we are going to wish to have a dense layer with two models.
... %>% layer_dense(models = 2, activation = "linear") %>%Then layer_distribution_lambda will use the primary unit because the imply of a traditional distribution, and the second as its customary deviation.
layer_distribution_lambda(perform(x)
tfd_normal(loc = x[, 1, drop = FALSE],
scale = 1e-3 + tf$math$softplus(x[, 2, drop = FALSE])
)
)Right here is the whole mannequin we use. We insert an extra dense layer in entrance, with a relu activation, to offer the mannequin a bit extra freedom and capability. We talk about this, in addition to that scale = ... foo, as quickly as we’ve completed our walkthrough of mannequin coaching.
mannequin <- keras_model_sequential() %>%
layer_dense(models = 8, activation = "relu") %>%
layer_dense(models = 2, activation = "linear") %>%
layer_distribution_lambda(perform(x)
tfd_normal(loc = x[, 1, drop = FALSE],
# ignore on first learn, we'll come again to this
# scale = 1e-3 + 0.05 * tf$math$softplus(x[, 2, drop = FALSE])
scale = 1e-3 + tf$math$softplus(x[, 2, drop = FALSE])
)
)For a mannequin that outputs a distribution, the loss is the unfavourable log chance given the goal knowledge.
negloglik <- perform(y, mannequin) - (mannequin %>% tfd_log_prob(y))We will now compile and match the mannequin.
We now name the mannequin on the take a look at knowledge to acquire the predictions. The predictions now really are distributions, and we’ve 150 of them, one for every datapoint:
yhat <- mannequin(tf$fixed(x_test))tfp.distributions.Regular("sequential/distribution_lambda/Regular/",
batch_shape=[150, 1], event_shape=[], dtype=float32)To acquire the means and customary deviations – the latter being that measure of aleatoric uncertainty we’re fascinated with – we simply name tfd_mean and tfd_stddev on these distributions.
That can give us the anticipated imply, in addition to the anticipated variance, per datapoint.
Let’s visualize this. Listed below are the precise take a look at knowledge factors, the anticipated means, in addition to confidence bands indicating the imply estimate plus/minus two customary deviations.
ggplot(knowledge.body(
x = x,
y = y,
imply = as.numeric(imply),
sd = as.numeric(sd)
),
aes(x, y)) +
geom_point() +
geom_line(aes(x = x_test, y = imply), shade = "violet", dimension = 1.5) +
geom_ribbon(aes(
x = x_test,
ymin = imply - 2 * sd,
ymax = imply + 2 * sd
),
alpha = 0.2,
fill = "gray")
Determine 2: Aleatoric uncertainty on simulated knowledge, utilizing relu activation within the first dense layer.
This seems fairly affordable. What if we had used linear activation within the first layer? That means, what if the mannequin had seemed like this:
This time, the mannequin doesn’t seize the “type” of the information that effectively, as we’ve disallowed any nonlinearities.

Determine 3: Aleatoric uncertainty on simulated knowledge, utilizing linear activation within the first dense layer.
Utilizing linear activations solely, we additionally must do extra experimenting with the scale = ... line to get the consequence look “proper”. With relu, then again, outcomes are fairly strong to adjustments in how scale is computed. Which activation can we select? If our aim is to adequately mannequin variation within the knowledge, we will simply select relu – and go away assessing uncertainty within the mannequin to a unique method (the epistemic uncertainty that’s up subsequent).
General, it looks as if aleatoric uncertainty is the simple half. We would like the community to be taught the variation inherent within the knowledge, which it does. What can we achieve? As a substitute of acquiring simply level estimates, which on this instance would possibly end up fairly dangerous within the two fan-like areas of the information on the left and proper sides, we be taught concerning the unfold as effectively. We’ll thus be appropriately cautious relying on what enter vary we’re making predictions for.
Epistemic uncertainty
Now our focus is on the mannequin. Given a speficic mannequin (e.g., one from the linear household), what sort of knowledge does it say conforms to its expectations?
To reply this query, we make use of a variational-dense layer.
That is once more a Keras layer offered by tfprobability. Internally, it really works by minimizing the proof decrease certain (ELBO), thus striving to search out an approximative posterior that does two issues:
- match the precise knowledge effectively (put in another way: obtain excessive log chance), and
- keep near a prior (as measured by KL divergence).
As customers, we really specify the type of the posterior in addition to that of the prior. Right here is how a previous may look.
prior_trainable <-
perform(kernel_size,
bias_size = 0,
dtype = NULL) {
n <- kernel_size + bias_size
keras_model_sequential() %>%
# we'll touch upon this quickly
# layer_variable(n, dtype = dtype, trainable = FALSE) %>%
layer_variable(n, dtype = dtype, trainable = TRUE) %>%
layer_distribution_lambda(perform(t) {
tfd_independent(tfd_normal(loc = t, scale = 1),
reinterpreted_batch_ndims = 1)
})
}This prior is itself a Keras mannequin, containing a layer that wraps a variable and a layer_distribution_lambda, that sort of distribution-yielding layer we’ve simply encountered above. The variable layer could possibly be mounted (non-trainable) or non-trainable, akin to a real prior or a previous learnt from the information in an empirical Bayes-like method. The distribution layer outputs a traditional distribution since we’re in a regression setting.
The posterior too is a Keras mannequin – positively trainable this time. It too outputs a traditional distribution:
posterior_mean_field <-
perform(kernel_size,
bias_size = 0,
dtype = NULL) {
n <- kernel_size + bias_size
c <- log(expm1(1))
keras_model_sequential(listing(
layer_variable(form = 2 * n, dtype = dtype),
layer_distribution_lambda(
make_distribution_fn = perform(t) {
tfd_independent(tfd_normal(
loc = t[1:n],
scale = 1e-5 + tf$nn$softplus(c + t[(n + 1):(2 * n)])
), reinterpreted_batch_ndims = 1)
}
)
))
}Now that we’ve outlined each, we will arrange the mannequin’s layers. The primary one, a variational-dense layer, has a single unit. The following distribution layer then takes that unit’s output and makes use of it for the imply of a traditional distribution – whereas the size of that Regular is mounted at 1:
You’ll have seen one argument to layer_dense_variational we haven’t mentioned but, kl_weight.
That is used to scale the contribution to the full lack of the KL divergence, and usually ought to equal one over the variety of knowledge factors.
Coaching the mannequin is simple. As customers, we solely specify the unfavourable log chance a part of the loss; the KL divergence half is taken care of transparently by the framework.
Due to the stochasticity inherent in a variational-dense layer, every time we name this mannequin, we get hold of totally different outcomes: totally different regular distributions, on this case.
To acquire the uncertainty estimates we’re in search of, we subsequently name the mannequin a bunch of instances – 100, say:
yhats <- purrr::map(1:100, perform(x) mannequin(tf$fixed(x_test)))We will now plot these 100 predictions – strains, on this case, as there are not any nonlinearities:
means <-
purrr::map(yhats, purrr::compose(as.matrix, tfd_mean)) %>% abind::abind()
strains <- knowledge.body(cbind(x_test, means)) %>%
collect(key = run, worth = worth,-X1)
imply <- apply(means, 1, imply)
ggplot(knowledge.body(x = x, y = y, imply = as.numeric(imply)), aes(x, y)) +
geom_point() +
geom_line(aes(x = x_test, y = imply), shade = "violet", dimension = 1.5) +
geom_line(
knowledge = strains,
aes(x = X1, y = worth, shade = run),
alpha = 0.3,
dimension = 0.5
) +
theme(legend.place = "none")
Determine 4: Epistemic uncertainty on simulated knowledge, utilizing linear activation within the variational-dense layer.
What we see listed here are primarily totally different fashions, per the assumptions constructed into the structure. What we’re not accounting for is the unfold within the knowledge. Can we do each? We will; however first let’s touch upon a number of decisions that had been made and see how they have an effect on the outcomes.
To stop this submit from rising to infinite dimension, we’ve shunned performing a scientific experiment; please take what follows not as generalizable statements, however as tips that could issues you’ll want to consider in your personal ventures. Particularly, every (hyper-)parameter shouldn’t be an island; they may work together in unexpected methods.
After these phrases of warning, listed here are some issues we seen.
- One query you would possibly ask: Earlier than, within the aleatoric uncertainty setup, we added an extra dense layer to the mannequin, with
reluactivation. What if we did this right here?
Firstly, we’re not including any further, non-variational layers with a purpose to hold the setup “absolutely Bayesian” – we would like priors at each stage. As to utilizingreluinlayer_dense_variational, we did strive that, and the outcomes look fairly comparable:

Determine 5: Epistemic uncertainty on simulated knowledge, utilizing relu activation within the variational-dense layer.
Nevertheless, issues look fairly totally different if we drastically scale back coaching time… which brings us to the subsequent commentary.
- Not like within the aleatoric setup, the variety of coaching epochs matter rather a lot. If we prepare, quote unquote, too lengthy, the posterior estimates will get nearer and nearer to the posterior imply: we lose uncertainty. What occurs if we prepare “too quick” is much more notable. Listed below are the outcomes for the linear-activation in addition to the relu-activation circumstances:

Determine 6: Epistemic uncertainty on simulated knowledge if we prepare for 100 epochs solely. Left: linear activation. Proper: relu activation.
Apparently, each mannequin households look very totally different now, and whereas the linear-activation household seems extra affordable at first, it nonetheless considers an total unfavourable slope per the information.
So what number of epochs are “lengthy sufficient”? From commentary, we’d say {that a} working heuristic ought to most likely be based mostly on the speed of loss discount. However definitely, it’ll make sense to strive totally different numbers of epochs and verify the impact on mannequin conduct. As an apart, monitoring estimates over coaching time could even yield essential insights into the assumptions constructed right into a mannequin (e.g., the impact of various activation features).
-
As essential because the variety of epochs educated, and comparable in impact, is the studying price. If we change the educational price on this setup by
0.001, outcomes will look much like what we noticed above for theepochs = 100case. Once more, we are going to wish to strive totally different studying charges and ensure we prepare the mannequin “to completion” in some affordable sense. -
To conclude this part, let’s rapidly have a look at what occurs if we differ two different parameters. What if the prior had been non-trainable (see the commented line above)? And what if we scaled the significance of the KL divergence (
kl_weightinlayer_dense_variational’s argument listing) in another way, changingkl_weight = 1/nbykl_weight = 1(or equivalently, eradicating it)? Listed below are the respective outcomes for an otherwise-default setup. They don’t lend themselves to generalization – on totally different (e.g., greater!) datasets the outcomes will most definitely look totally different – however positively attention-grabbing to look at.

Determine 7: Epistemic uncertainty on simulated knowledge. Left: kl_weight = 1. Proper: prior non-trainable.
Now let’s come again to the query: We’ve modeled unfold within the knowledge, we’ve peeked into the center of the mannequin, – can we do each on the identical time?
We will, if we mix each approaches. We add an extra unit to the variational-dense layer and use this to be taught the variance: as soon as for every “sub-model” contained within the mannequin.
Combining each aleatoric and epistemic uncertainty
Reusing the prior and posterior from above, that is how the ultimate mannequin seems:
mannequin <- keras_model_sequential() %>%
layer_dense_variational(
models = 2,
make_posterior_fn = posterior_mean_field,
make_prior_fn = prior_trainable,
kl_weight = 1 / n
) %>%
layer_distribution_lambda(perform(x)
tfd_normal(loc = x[, 1, drop = FALSE],
scale = 1e-3 + tf$math$softplus(0.01 * x[, 2, drop = FALSE])
)
)We prepare this mannequin identical to the epistemic-uncertainty just one. We then get hold of a measure of uncertainty per predicted line. Or within the phrases we used above, we now have an ensemble of fashions every with its personal indication of unfold within the knowledge. Here’s a method we may show this – every coloured line is the imply of a distribution, surrounded by a confidence band indicating +/- two customary deviations.
yhats <- purrr::map(1:100, perform(x) mannequin(tf$fixed(x_test)))
means <-
purrr::map(yhats, purrr::compose(as.matrix, tfd_mean)) %>% abind::abind()
sds <-
purrr::map(yhats, purrr::compose(as.matrix, tfd_stddev)) %>% abind::abind()
means_gathered <- knowledge.body(cbind(x_test, means)) %>%
collect(key = run, worth = mean_val,-X1)
sds_gathered <- knowledge.body(cbind(x_test, sds)) %>%
collect(key = run, worth = sd_val,-X1)
strains <-
means_gathered %>% inner_join(sds_gathered, by = c("X1", "run"))
imply <- apply(means, 1, imply)
ggplot(knowledge.body(x = x, y = y, imply = as.numeric(imply)), aes(x, y)) +
geom_point() +
theme(legend.place = "none") +
geom_line(aes(x = x_test, y = imply), shade = "violet", dimension = 1.5) +
geom_line(
knowledge = strains,
aes(x = X1, y = mean_val, shade = run),
alpha = 0.6,
dimension = 0.5
) +
geom_ribbon(
knowledge = strains,
aes(
x = X1,
ymin = mean_val - 2 * sd_val,
ymax = mean_val + 2 * sd_val,
group = run
),
alpha = 0.05,
fill = "gray",
inherit.aes = FALSE
)
Determine 8: Displaying each epistemic and aleatoric uncertainty on the simulated dataset.
Good! This seems like one thing we may report.
As you may think, this mannequin, too, is delicate to how lengthy (assume: variety of epochs) or how briskly (assume: studying price) we prepare it. And in comparison with the epistemic-uncertainty solely mannequin, there’s an extra option to be made right here: the scaling of the earlier layer’s activation – the 0.01 within the scale argument to tfd_normal:
scale = 1e-3 + tf$math$softplus(0.01 * x[, 2, drop = FALSE])Holding all the pieces else fixed, right here we differ that parameter between 0.01 and 0.05:

Determine 9: Epistemic plus aleatoric uncertainty on the simulated dataset: Various the size argument.
Evidently, that is one other parameter we ought to be ready to experiment with.
Now that we’ve launched all three varieties of presenting uncertainty – aleatoric solely, epistemic solely, or each – let’s see them on the aforementioned Mixed Cycle Energy Plant Information Set. Please see our earlier submit on uncertainty for a fast characterization, in addition to visualization, of the dataset.
Mixed Cycle Energy Plant Information Set
To maintain this submit at a digestible size, we’ll chorus from attempting as many options as with the simulated knowledge and primarily stick with what labored effectively there. This must also give us an concept of how effectively these “defaults” generalize. We individually examine two eventualities: The one-predictor setup (utilizing every of the 4 out there predictors alone), and the whole one (utilizing all 4 predictors without delay).
The dataset is loaded simply as within the earlier submit.
First we have a look at the single-predictor case, ranging from aleatoric uncertainty.
Single predictor: Aleatoric uncertainty
Right here is the “default” aleatoric mannequin once more. We additionally duplicate the plotting code right here for the reader’s comfort.
n <- nrow(X_train) # 7654
n_epochs <- 10 # we want fewer epochs as a result of the dataset is a lot greater
batch_size <- 100
learning_rate <- 0.01
# variable to suit - change to 2,3,4 to get the opposite predictors
i <- 1
mannequin <- keras_model_sequential() %>%
layer_dense(models = 16, activation = "relu") %>%
layer_dense(models = 2, activation = "linear") %>%
layer_distribution_lambda(perform(x)
tfd_normal(loc = x[, 1, drop = FALSE],
scale = tf$math$softplus(x[, 2, drop = FALSE])
)
)
negloglik <- perform(y, mannequin) - (mannequin %>% tfd_log_prob(y))
mannequin %>% compile(optimizer = optimizer_adam(lr = learning_rate), loss = negloglik)
hist <-
mannequin %>% match(
X_train[, i, drop = FALSE],
y_train,
validation_data = listing(X_val[, i, drop = FALSE], y_val),
epochs = n_epochs,
batch_size = batch_size
)
yhat <- mannequin(tf$fixed(X_val[, i, drop = FALSE]))
imply <- yhat %>% tfd_mean()
sd <- yhat %>% tfd_stddev()
ggplot(knowledge.body(
x = X_val[, i],
y = y_val,
imply = as.numeric(imply),
sd = as.numeric(sd)
),
aes(x, y)) +
geom_point() +
geom_line(aes(x = x, y = imply), shade = "violet", dimension = 1.5) +
geom_ribbon(aes(
x = x,
ymin = imply - 2 * sd,
ymax = imply + 2 * sd
),
alpha = 0.4,
fill = "gray")How effectively does this work?

Determine 10: Aleatoric uncertainty on the Mixed Cycle Energy Plant Information Set; single predictors.
This seems fairly good we’d say! How about epistemic uncertainty?
Single predictor: Epistemic uncertainty
Right here’s the code:
posterior_mean_field <-
perform(kernel_size,
bias_size = 0,
dtype = NULL) {
n <- kernel_size + bias_size
c <- log(expm1(1))
keras_model_sequential(listing(
layer_variable(form = 2 * n, dtype = dtype),
layer_distribution_lambda(
make_distribution_fn = perform(t) {
tfd_independent(tfd_normal(
loc = t[1:n],
scale = 1e-5 + tf$nn$softplus(c + t[(n + 1):(2 * n)])
), reinterpreted_batch_ndims = 1)
}
)
))
}
prior_trainable <-
perform(kernel_size,
bias_size = 0,
dtype = NULL) {
n <- kernel_size + bias_size
keras_model_sequential() %>%
layer_variable(n, dtype = dtype, trainable = TRUE) %>%
layer_distribution_lambda(perform(t) {
tfd_independent(tfd_normal(loc = t, scale = 1),
reinterpreted_batch_ndims = 1)
})
}
mannequin <- keras_model_sequential() %>%
layer_dense_variational(
models = 1,
make_posterior_fn = posterior_mean_field,
make_prior_fn = prior_trainable,
kl_weight = 1 / n,
activation = "linear",
) %>%
layer_distribution_lambda(perform(x)
tfd_normal(loc = x, scale = 1))
negloglik <- perform(y, mannequin) - (mannequin %>% tfd_log_prob(y))
mannequin %>% compile(optimizer = optimizer_adam(lr = learning_rate), loss = negloglik)
hist <-
mannequin %>% match(
X_train[, i, drop = FALSE],
y_train,
validation_data = listing(X_val[, i, drop = FALSE], y_val),
epochs = n_epochs,
batch_size = batch_size
)
yhats <- purrr::map(1:100, perform(x)
yhat <- mannequin(tf$fixed(X_val[, i, drop = FALSE])))
means <-
purrr::map(yhats, purrr::compose(as.matrix, tfd_mean)) %>% abind::abind()
strains <- knowledge.body(cbind(X_val[, i], means)) %>%
collect(key = run, worth = worth,-X1)
imply <- apply(means, 1, imply)
ggplot(knowledge.body(x = X_val[, i], y = y_val, imply = as.numeric(imply)), aes(x, y)) +
geom_point() +
geom_line(aes(x = X_val[, i], y = imply), shade = "violet", dimension = 1.5) +
geom_line(
knowledge = strains,
aes(x = X1, y = worth, shade = run),
alpha = 0.3,
dimension = 0.5
) +
theme(legend.place = "none")And that is the consequence.

Determine 11: Epistemic uncertainty on the Mixed Cycle Energy Plant Information Set; single predictors.
As with the simulated knowledge, the linear fashions appears to “do the suitable factor”. And right here too, we predict we are going to wish to increase this with the unfold within the knowledge: Thus, on to method three.
Single predictor: Combining each varieties
Right here we go. Once more, posterior_mean_field and prior_trainable look identical to within the epistemic-only case.
mannequin <- keras_model_sequential() %>%
layer_dense_variational(
models = 2,
make_posterior_fn = posterior_mean_field,
make_prior_fn = prior_trainable,
kl_weight = 1 / n,
activation = "linear"
) %>%
layer_distribution_lambda(perform(x)
tfd_normal(loc = x[, 1, drop = FALSE],
scale = 1e-3 + tf$math$softplus(0.01 * x[, 2, drop = FALSE])))
negloglik <- perform(y, mannequin)
- (mannequin %>% tfd_log_prob(y))
mannequin %>% compile(optimizer = optimizer_adam(lr = learning_rate), loss = negloglik)
hist <-
mannequin %>% match(
X_train[, i, drop = FALSE],
y_train,
validation_data = listing(X_val[, i, drop = FALSE], y_val),
epochs = n_epochs,
batch_size = batch_size
)
yhats <- purrr::map(1:100, perform(x)
mannequin(tf$fixed(X_val[, i, drop = FALSE])))
means <-
purrr::map(yhats, purrr::compose(as.matrix, tfd_mean)) %>% abind::abind()
sds <-
purrr::map(yhats, purrr::compose(as.matrix, tfd_stddev)) %>% abind::abind()
means_gathered <- knowledge.body(cbind(X_val[, i], means)) %>%
collect(key = run, worth = mean_val,-X1)
sds_gathered <- knowledge.body(cbind(X_val[, i], sds)) %>%
collect(key = run, worth = sd_val,-X1)
strains <-
means_gathered %>% inner_join(sds_gathered, by = c("X1", "run"))
imply <- apply(means, 1, imply)
#strains <- strains %>% filter(run=="X3" | run =="X4")
ggplot(knowledge.body(x = X_val[, i], y = y_val, imply = as.numeric(imply)), aes(x, y)) +
geom_point() +
theme(legend.place = "none") +
geom_line(aes(x = X_val[, i], y = imply), shade = "violet", dimension = 1.5) +
geom_line(
knowledge = strains,
aes(x = X1, y = mean_val, shade = run),
alpha = 0.2,
dimension = 0.5
) +
geom_ribbon(
knowledge = strains,
aes(
x = X1,
ymin = mean_val - 2 * sd_val,
ymax = mean_val + 2 * sd_val,
group = run
),
alpha = 0.01,
fill = "gray",
inherit.aes = FALSE
)And the output?

Determine 12: Mixed uncertainty on the Mixed Cycle Energy Plant Information Set; single predictors.
This seems helpful! Let’s wrap up with our last take a look at case: Utilizing all 4 predictors collectively.
All predictors
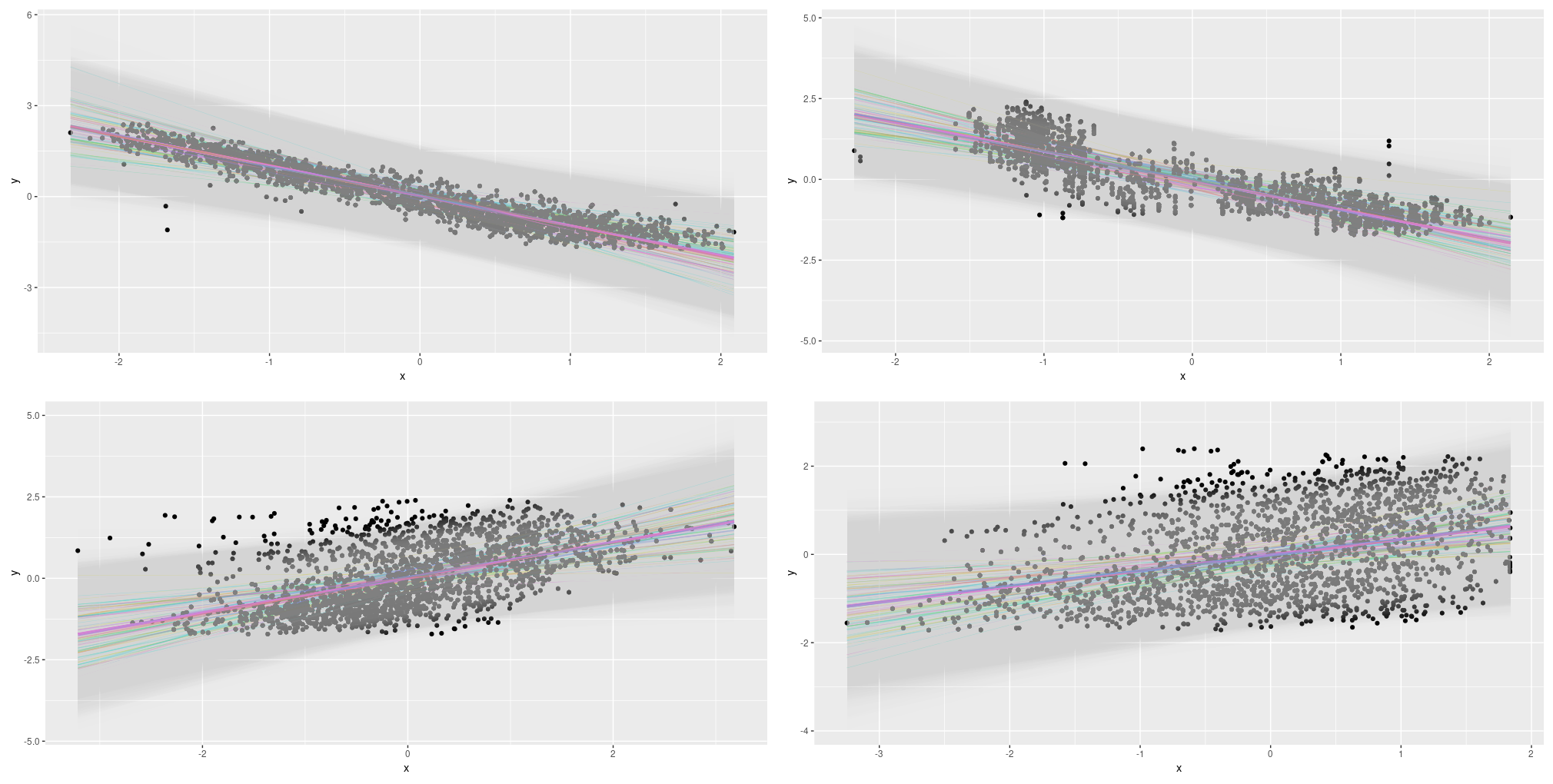
The coaching code used on this state of affairs seems identical to earlier than, other than our feeding all predictors to the mannequin. For plotting, we resort to displaying the primary principal element on the x-axis – this makes the plots look noisier than earlier than. We additionally show fewer strains for the epistemic and epistemic-plus-aleatoric circumstances (20 as a substitute of 100). Listed below are the outcomes:

Determine 13: Uncertainty (aleatoric, epistemic, each) on the Mixed Cycle Energy Plant Information Set; all predictors.
Conclusion
The place does this go away us? In comparison with the learnable-dropout method described within the prior submit, the way in which offered here’s a lot simpler, quicker, and extra intuitively comprehensible.
The strategies per se are that straightforward to make use of that on this first introductory submit, we may afford to discover options already: one thing we had no time to do in that earlier exposition.
Actually, we hope this submit leaves you ready to do your personal experiments, by yourself knowledge.
Clearly, you’ll have to make choices, however isn’t that the way in which it’s in knowledge science? There’s no method round making choices; we simply ought to be ready to justify them …
Thanks for studying!