T-test: The most well-liked speculation check
In immediately’s data-driven world, information is generated and consumed every day. All this information holds numerous hidden concepts and knowledge that may be exhausting to uncover. Information scientists generally strategy this drawback utilizing statistics to make educated guesses about information.
Any testable assumption relating to information is known as a speculation. Speculation testing is a statistical testing methodology used to experimentally confirm a speculation. In information science, speculation testing examines assumptions on pattern information to attract insights a couple of bigger information inhabitants.
Speculation testing varies primarily based on the statistical inhabitants parameter getting used for testing. One of the vital widespread issues in statistics is evaluating the means between two populations. The commonest strategy to that is the t-test. On this article, we’ll focus on about this in style statistical check and present some easy examples within the Python programming language.
What’s a T-Check?
The t-test was developed by William Sealy Gosset in 1908 as Pupil’s t-test. Sealy printed his work underneath the pseudonym “Pupil”. The target of this check is to match the technique of two associated or unrelated pattern teams. It’s utilized in speculation testing to check the applicability of an assumption to a inhabitants of curiosity. T-tests are solely relevant to 2 information teams. If you wish to examine greater than two teams, then you need to resort to different assessments similar to ANOVA.

When are T-Exams used?
A one-tailed t-test is a directional check that determines the connection between inhabitants means in a single course, i.e., proper or left tail. A two-tailed t-test is a non-directional check that determines if there’s any relationship between inhabitants means in both course.
So once you count on a single worth speculation, like mean1=mean2, a one-tailed check could be preferable. A two-tailed check makes extra sense in case your speculation assumes means to be higher than or lower than one another.
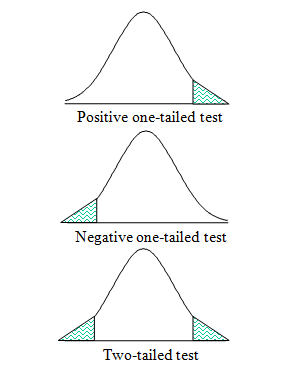
What are the assumptions?
T-tests are parametric assessments for figuring out correlations between two samples of knowledge. T-tests require information to be distributed based on the next assumptions about unknown inhabitants parameters:
- Information values are unbiased and steady, i.e., the measurement scale for information ought to observe a steady sample.
- Information is usually distributed, i.e., when plotted, its graph resembles a bell-shaped curve.
- Information is randomly sampled.
- Variance of knowledge in each pattern teams is comparable, i.e., samples have nearly equal customary deviation (relevant for a two-sample t-test).
What are the steps concerned in T-Exams?
Like every speculation check, t-tests are carried out within the following order of steps:
- State a speculation. A speculation is classed as a null speculation ( H0) and another speculation (Ha) that rejects the null speculation. The null and alternate hypotheses are outlined based on the kind of check being carried out.
- Accumulate pattern information.
- Conduct the check.
- Reject or fail to reject your null speculation H0.

What are the parameters concerned in T-tests?
Along with group means and customary deviations, there are different parameters in t-tests which might be concerned in figuring out the validity of the null speculation. Following is an inventory of these parameters that may repeatedly be talked about forward when implementing t-tests:
- T-statistic: A t-test reduces your complete information right into a single worth, referred to as the t-statistic. This single worth serves as a measure of proof in opposition to the acknowledged speculation. A t-statistic near zero represents the bottom proof in opposition to the speculation. A bigger t-statistic worth represents sturdy proof in opposition to the speculation.
- P-value: A p-value is the share likelihood of the t-statistic to have occurred by likelihood. It’s represented as a decimal, e.g., a p-value of 0.05 represents a 5% likelihood of seeing a t-statistic no less than as excessive because the one calculated, assuming the null speculation was true.
- Significance stage: A significance stage is the share likelihood of rejecting a real null speculation. That is additionally referred to as alpha.
What are the various kinds of T-Exams?
There are three principal kinds of t-tests relying on the quantity and sort of pattern teams concerned. Allow us to get into the main points and implementation of every sort:
1. One-Pattern T-Check
An one-sample t-test compares the imply of a pattern group to a hypothetical imply worth. This check is carried out on a single pattern group, therefore the title; one-sample check. The check goals to determine whether or not the pattern group belongs to the hypothetical inhabitants.
System
t=m-s/nWhere,t= T-statisticm= group imply= preset imply worth (theoretical or imply of the inhabitants)s= group customary deviationn= measurement of group
Implementation
Step 1: Outline hypotheses for the check (null and different)
State the next hypotheses:
- Null Speculation (H0): Pattern imply (m) is lower than or equal to the hypothetical imply. (<=m)
- Different Speculation (Ha): Pattern imply (m) is larger than the hypothetical imply. (>m)
Step 2: Import Python libraries
Begin with importing required libraries. In Python, stats library is used for t-tests that embrace the ttest_1samp operate to carry out a one-sample t-test.
import numpy as np from scipy import stats from numpy.random import seed from numpy.random import randn from numpy.random import regular from scipy.stats import ttest_1samp
Step 3: Create a random pattern group
Create a random pattern group of 20 values utilizing the traditional operate within the numpy.random library. Setting the imply to 150 and customary deviation to 10.
seed=(1) pattern =regular(150,10,20) print(‘Pattern: ‘, pattern)
Step 4: Conduct the check
Use the ttest_1samp operate to conduct a one-sample t-test. Set the popmean parameter to 155 based on the null speculation (pattern imply<=inhabitants imply). This operate returns a t-statistic worth and a p-value and performs a two-tailed check by default. To get a one-tailed check end result, divide the p-value by 2 and examine in opposition to a significance stage of 0.05 (additionally referred to as alpha).
t_stat, p_value = ttest_1samp(pattern, popmean=155) print(“T-statistic worth: “, t_stat) print(“P-Worth: “, p_value)
A destructive t-value signifies the course of the pattern imply excessive, and has no impact on the distinction between pattern and inhabitants means.
Step 5: Examine standards for rejecting the null speculation
For the null speculation, assuming the pattern imply is lesser than or equal to the hypothetical imply:
- Reject the null speculation if p-value <= alpha
- Fail to reject the null speculation if p-value > alpha
- Reject or fail to reject speculation primarily based on end result
The outcomes point out a p-value of 0.21, which is larger than = 0.05, failing to reject the null speculation. So this check concludes that the pattern imply was lower than the hypothetical imply.
2. Two-Pattern T-test
A two-sample t-test, often known as an independent-sample check, compares the technique of two unbiased pattern teams. A two-sample t-test goals to match the technique of samples belonging to 2 completely different populations.
System
t=mA- mBs2nA+s2nBWhere,mA and mB = technique of the 2 samplesnA and nB = sizes of the 2 sampless2 = widespread variance of the 2 samples
Implementation
Step 1: Outline the hypotheses (null and different)
State the next hypotheses for significance stage =0.05:
- Null Speculation (H0): Impartial pattern means (m1 and m2) are equal. (m1=m2)
- Different Speculation (Ha): Impartial pattern means (m1 and m2) aren’t equal. (m1!=m2)
Step 2: Import libraries
Begin with importing required libraries. Like beforehand, stats library is used for t-tests that embrace the ttest_ind operate to carry out unbiased pattern t-test (two-sample check).
from numpy.random import seed from numpy.random import randn from numpy.random import regular from scipy.stats import ttest_ind
Step 3: Create two unbiased pattern teams
Utilizing the regular operate of the random quantity generator to create two usually distributed unbiased samples of fifty values, completely different means (30 and 33), and nearly the identical customary deviations (16 and 18).
# seed the random quantity generator seed(1) # create two unbiased pattern teams sample1= regular(30, 16, 50) sample2=regular(33, 18, 50) print(‘Pattern 1: ‘,sample1) print(‘Pattern 2: ‘,sample2)
Step 4: Conduct the check
Use the ttest_ind operate to conduct a two-sample t-test. This operate returns a t-statistic worth and a p-value.
t_stat, p_value = ttest_ind(sample1, sample2) print(“T-statistic worth: “, t_stat) print(“P-Worth: “, p_value)
Step 5: Examine standards for rejecting the null speculation
For the null speculation, assuming pattern means are equal:
- Reject the null speculation if p-value <= alpha
- Fail to reject the null speculation if p-value > alpha
- Reject or fail to reject every speculation primarily based on the end result
The outcomes point out a p-value of 0.04, which is lower than alpha=0.05, rejecting the null speculation. So this two-sample t-test concludes that the imply of the primary pattern is both higher or lower than the imply of the second pattern.
3. Paired T-Check
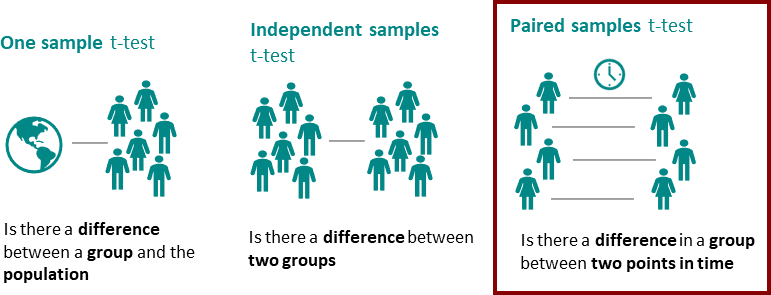
A paired t-test, often known as a dependent pattern check, compares the technique of two associated samples. The samples belong to the identical inhabitants and are analyzed underneath various circumstances, e.g., at completely different time limits. This check is usually in style for pretest/posttest sort of experiments the place a pattern is studied earlier than and after its circumstances are various with an experiment.
System
t=ms/nWhere,t= T-statisticm= group means= group customary deviationn= measurement of group
Implementation
Step 1: Outline hypotheses (null and different)
State the next hypotheses for significance stage =0.05:
- Null Speculation (H0): Dependent pattern means (m1 and m2) are equal (m1=m2).
- Different Speculation (Ha): Dependent pattern means (m1 and m2) aren’t equal (m1!=m2)
Step 2: Import Python libraries
Begin with importing required libraries. Import the ttest_rel operate from the stats library to carry out a dependent pattern t-test (paired t-test).
from numpy.random import seed from numpy.random import randn from numpy.random import regular from scipy.stats import ttest_rel
Step 3: Create two dependent pattern teams
For simplicity, use the identical random samples from the two-sample implementation. We will assume the samples are from the identical inhabitants.
# seed the random quantity generator seed(1) # create two dependent pattern teams sample1= regular(30, 16, 50) sample2=regular(33, 18, 50) print(‘Pattern 1: ‘,sample1) print(‘Pattern 2: ‘,sample2)
Step 4: Conduct the check
Use ttest_rel operate to conduct a two-sample t-test on two dependent/associated samples. This operate returns a t-statistic worth and a p-value.
t_stat, p_value = ttest_rel(sample1, sample2) print(“T-statistic worth: “, t_stat) print(“P-Worth: “, p_value)
Step 5: Examine standards for rejecting the null speculation
For the null speculation assuming pattern means are equal:
- Reject the null speculation if p-value <= alpha
- Fail to reject the null speculation if p-value > alpha
- Reject or fail to reject speculation primarily based on end result
The outcomes point out a p-value of 0.05, which is the same as 0.05, therefore rejecting the null speculation. So this paired t-test concludes that the imply of the primary pattern is both higher or lower than the imply of the second pattern.
Why are t-tests helpful in information evaluation?
The t-test is a flexible instrument. Information scientists use these assessments to confirm their information observations and the likelihood of these observations being true. It’s a tried-and-tested strategy to evaluating observations with out the overhead of involving your complete inhabitants information within the evaluation.
From testing the acquisition numbers of a brand new product to evaluating financial progress amongst nations, speculation assessments are an vital statistical instrument for companies and one of the vital vital instruments in a statistician’s arsenal. Wherever information is concerned, t-tests will play a vital position in validating information findings.
If you’re curious about pursuing a profession in information science, make sure that to take a look at Past Machine!
The submit Tips on how to Do a T-test in Python? appeared first on Datafloq.

